Didactique
Groupes de recherche :
Didactique Montpellier
Responsable : Aurélie Chesnais
Membres :
CERCLE, Véronique ; CONSTANTIN, Céline ; DELAMARE, Aimée ; DESTRIBATS, Aurélien ; DUTAUT, Sophie ; LAHMOUCHE, Nazha ; LEFAUCHEUR, Jérémie; LEFORT, Julie ; NYSSEN, Louise.
Nous avons également accueilli une stagiaire de M2 Didactique des Sciences durant toute l’année, Maëlis Béjaud. Son mémoire de master a porté sur les élèves dans une classe d’une des participant.es du groupe, dans les séances de classe liées au travail du groupe.
Travaux du groupe en 2023-2024 :
Résumé:
Le groupe a poursuivi le travail engagé depuis six années sur la question du rôle du langage dans l’enseignement et l’apprentissage des mathématiques. La question de départ concernait la difficulté pour l’enseignant de concilier l’exigence d’une certaine rigueur du langage mathématique (en référence au savoir savant) avec l’utilisation de certains « abus de langage » inhérents aux pratiques langagières expertes.
Il est rapidement apparu que ces « abus de langage » ne sont qu’une partie des formes langagières expertes (mobilisant le langage naturel ou le langage symbolique), porteuses d’une certaine économie. Ces pratiques expertes doivent constituer un horizon dans l’apprentissage et leur utilisation de façon trop précoce est probablement potentiellement porteuse de malentendus ou de difficultés pour les élèves. Ces réflexions nous ont amenés à émettre des hypothèses sur le fonctionnement du développement du langage (certaines formes mobilisant le langage naturel ou d’autres, le langage symbolique) dans la classe lors de l’introduction de nouveaux objets d’apprentissage. Nous nous intéressons en particulier depuis quatre ans d’une part aux formulations (en langage naturel) liées à la notion de distance au début du collège, d’autres part aux notations utilisées pour les suites numériques au lycée. Nous nous y intéressons à la fois en tant qu’objets d’apprentissage et de moyens d’apprentissages, comme supports du processus de conceptualisation. Nos questionnements portent sur le repérage des difficultés d’apprentissage pour les élèves, ainsi que l’identification de leviers pour l’enseignement et pour la formation des enseignants, notamment en questionnant le rôle des discours (oraux et écrits) qui accompagnent ces processus.
Nous avons poursuivi cette année des expérimentations dans des classes de sixième et de cinquième sur les thèmes de la distance et du cercle. Des pré-tests et post-tests ont de nouveau été réalisés dans des classes de sixième, à la fois dans des classes des enseignants du groupe (6 classes) et dans des classes jouant alors le rôle de « classes témoins » (9 classes). L’analyse des productions des élèves dans les tests et de quelques éléments de séances de classes ont déjà produit des résultats intéressants, qui ont fait l’objet d’un article soumis à la revue suisse d’interface Revue Maths école (Rmé).
Nous nous intéressons en particulier depuis 2 ans d’une part aux formulations (en langage naturel) liées au cercle et à la notion de distance au début du collège, d’autre part aux notations utilisées pour les suites numériques au lycée. Nos questionnements portent sur le repérage des difficultés d’apprentissage pour les élèves, ainsi que l’identification de leviers pour l’enseignement et pour la formation des enseignants.
Nous avons par ailleurs poursuivi l’exploration du thème des suites et de la construction de la signification des notations. Nous avons finalisé les analyses d’une séquence mise en oeuvre et filmée dans une classe de Première spécialité sur les suites ainsi que des données recueillies en formation d’enseignants: des productions sur des exercices de mathématiques et des tâches d’analys didactique de supports concernant les suites, lors de séances de formation en M2 du master MEEF second degré mathématiques. Un nouveau recueil de données a été réalisé dans le prolongement de ce travail dans des classes de Terminale et deux enseignants du groupe (vidéos de classe et tests auprès d’élèves), afin de poursuivre la réflexion engagée autour du développement des discours susceptibles de favoriser des prises en charge des difficultés identifiées. L’année a également été l’occasion de rédiger les aces de l’atelier réalisé au colloque annuel de la Commission de Recherche sur le Formation des Enseigannts de Mathématiques (CORFEM) à Nantes en juin 2023.
Rayonnement :
Le travail mené au collège a nourri la présentation d’Aurélie Chesnais au colloque ICME 2024 à Sydney: Language and conceptual development in mathematics learning and teaching.
Il alimente par ailleurs les formations dispensées en masters MEEF par Aurélie Chesnais, Céline Constantin, Louise Nyssen et Véronique Cerclé.
Formation:
Une formation a été réalisée au PAF par Véronique Cerclé et Aurélie Chesnais sur la base des travaux du groupe, dont l’objectif est de faire travailler les enseignants sur les apports de la didactique à l’enseignement des mathématiques.
Publications:
Céline CONSTANTIN, Véronique CERCLE, Sophie DUTATUT, Jérémie LEFAUCHEUR, Louise NYSSEN. Que devient la variable lorsqu’elle est écrite en indice? Les suites numériques au lycée, entre nouvelles notations et techniques de calcul anciennes. Actes d’un atelier au colloque de la CORFEM.
Un article sur les travaux du groupe, avec une publication envisagée dans la revue Petit x est en cours de rédaction. Une proposition d’atelier devrait être soumise à la CORFEM 2025 sur le thème du travail collaboratif chercheurs-enseignants.
Travaux du groupe en 2021-2022
Ils sont passés par ce groupe :
PRAG, Université de Montpellier : Muriel Bourgeois
Professeurs de mathématiques : Fabrice Bonicel, Marc Boullis, Michel Bourguet, Laurence De Zanet, Nathalie Daval, Antoine-Liouba Leroux, Sylvie Pellequer (retraitée), Elisabeth Rebillard
Didactique Perpignan
Membres :
PRCE : Jérôme Ciavaldini, Marie-Claire Demailly, Julien Gravas, Séabstien Latour (formateur Master MEEF), Karine Le-Men, Cécile Bayramian.
PRAG: Nathalie Carbonell (formatrice Master MEEF), Armand Lachand
MCF: Eleda Robo
Retraitée: Pascale Boulais
Travaux du groupe en 2023-2024 :
1- Préparation en vue de la diffusion des travaux du groupe sur la pensée algébrique: Stage au PAF animé par Marie-Claire Demailly et Jérôme Ciavaldini sur l’entrée dans la pensée algébrique.
Dans l’objectif de développer la compétence algébrique au collège notre groupe a créé deux situations prenant appui sur les résultats de la recherche en didactique pour concevoir, expérimenter et scénariser des dispositifs d’enseignement :
- Une première favorisant l’entrée dans la pensée algébrique (somme des 10 entiers consécutifs)
- Une seconde favorisant l’apprentissage des propriétés du calcul algébrique (les 4 quatre) et le développement de la compétence algébrique au collège.
Toutes deux se voulant très accessibles aux élèves du collège avec comme prérequis le calcul sur les entiers. Ces deux situations ont été diffusées lors de trois journées, deux journées en présentiel et une en distanciel.
Illustration 1
Trouve le plus rapidement la somme des 10 nombres entiers consécutifs (les séries sont données aux élèves de manière successive) :
| 1ère série 17 – 18 – 19 – 20 – 21 – 22 – 23 – 24 – 25 – 26 | 3ème série 47 – 48 – 49 – 50 – 51 – 52 – 53 – 54 – 55 – 56 |
| 2ème série 23 – 24 – 25 – 26 – 27 – 28 – 29 – 30 – 31 – 32 | 4ème série 90 – 91 – 92 – 93 – 94 – 95 – 96 – 97 – 98 – 99 |
Illustration 2
Trouve -t-on toujours le même entier si on remplace les 4 par d’autres nombres entiers?
4 X 4 – 4 X 4 = 0
(4 – 4): 4 + 4 = 4
(4 – 4)X 4 + 4 = 4
(4 : 4)X 4 + 4 = 8
2- Poursuite du travail sur l’entrée dans la pensée fonctionnelle dans le cadre du 3ème appel à projets de l’INSPE de l’académie de Montpellier « Articulation/Recherche/Formation/Terrain ».
Nous avons enrichi et modifié la situation créée lors de l’exercice 2022/2023, puis nous l’avons testé dans 3 collèges accueillant des publics variés. L’écriture d’un compte-rendu de nos travaux sur ce sujet est un projet de l’année 2024/2025.
Notre projet sur l’entrée dans la pensée fonctionnelle rentre dans la continuité de notre travail sur l’entrée dans la pensée algébrique. Comme le montre ROBERT-SQUALLI-MARCHANT (EMF 2022), la pensée fonctionnelle est souvent restreinte à l’enrichissement des tâches algébriques ce qui restreint son propre développement. Nous émettons l’hypothèse que cette restriction est une des raisons pour lesquelles les élèves peinent à construire le concept de fonction en fin de collège et au lycée.
Nous avons travaillé sur une situation développant la pensée fonctionnelle pour elle-même hors du cadre de l’algèbre.
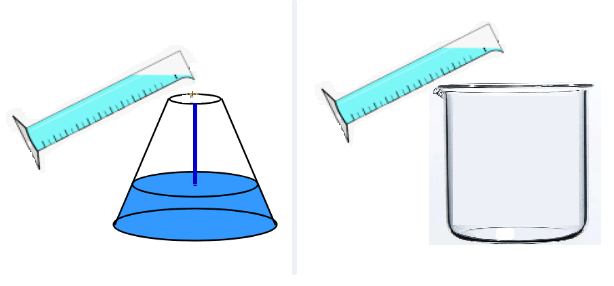
Le travail se déroule en classe autour de trois phases :
- Une phase d’appropriation du matériel et du vocabulaire à travers une question qui peut diviser la classe.
- Une phase de mesures pendant laquelle la covariation de deux grandeurs entre en jeu (la hauteur et le volume d’eau). Ces mesures sont classées suivant un premier registre représentant cette covariation : le tableau. La flèche de correspondance « ↦ » est introduite pour matérialiser la correspondance entre deux valeurs et éviter l’utilisation inappropriée du signe « = ».
- Une phase de recherche (sans utilisation de matériel) pour prévoir la hauteur de l’eau dans le bécher et dans le bol correspondant à un volume donné (et inversement). Cette dernière phase introduit un autre registre de représentation de la covariation (graphique) ainsi que deux classes de fonctions.
3- Relecture pour Viviane Durand-Guerrier et Françoise Monnoyeur du chapitre 4 de l’ouvrage sur l’infini.
Le groupe avait précédemment participer à une expérimentation sur les différences et les relations entre infini potentiel et infini actuel à travers la situation « Des carrés, encore des carrés … », une des activités décrites dans cet ouvrage. Nous avons cette année, accompagné par Simon modeste, participé à la relecture du chapitre 4.
4- Nouveau projet de recherche: transitions entre le collège et le lycée à travers la notion d’équation de courbe.
Les équations de courbes constituent au lycée non seulement une source de difficultés pour les élèves, mais aussi et surtout une occasion d’enrichir les conceptions des élèves en ce qui concerne tant les équations que les courbes. Nous souhaiterions comprendre l’origine de ses difficultés et créer une situation à la jonction des programmes de 3ème et de 2nde qui pourrait aider à les réguler.
| Liste des formations proposées: L’utilisation dans le cadre du master MEEF des activités travaillées au sein du groupe permettant un accompagnement didactique sur la différentiation et l’évaluation par compétence à travers les TICE. Stage au PAF animé par Marie-Claire Demailly et Jérôme CIAVALDINI sur l’entrée dans la pensée algébrique. |
| Les évolutions de carrières des membres du groupe: Jérôme CIAVALDINI, Marie-Claire Demailly et Armand Lachand vont intervenir en tant que vacataire dans le Master MEEF de Perpignan. La participation en elle-même au groupe IREM des personnes inscrites est une évolution de carrière dans le sens ou chacune progresse, apprend et diffuse dans leur établissement. |
| Les actions de diffusion en milieu scolaire ou grand public: L’utilisation dans le cadre du master MEEF des activités travaillées au sein du groupe permettant un accompagnement didactique sur la différentiation et l’évaluation par compétence à travers les TICE. |
| Les actions à venir: -Participation au PAF 2024/2025 sur l’entrée dans la pensée algébrique -Ecriture d’un compte-rendu de nos travaux sur l’entrée dans la pensée algébrique. -Ecriture d’un compte-rendu de nos travaux sur l’entrée dans la pensée fonctionnelle. -Nous sommes convaincus de l’intérêt de notre activité pour le développement de la pensée fonctionnelle, cependant le matériel nécessaire pour sa mise en œuvre peut nuire à sa prise en main par le corps enseignant. Aussi nous allons réfléchir à la rendre davantage « transportable ». |
Travaux du groupe en 2021-2022
Ils sont passés par ce groupe :
Professeurs de mathématiques : Marie Diumenge, Anne Lesobre, Claudine Vergne (retraitée), Catherine Sunye, Patrick Billard